I am a research scientist at Meta on the Central Applied Science team. Within Core Data Science, I work in the Adaptive Experimentation research group. My research focuses on methods for principled, sample-efficient optimization including Bayesian optimization and transfer learning. I am a co-creator of BoTorch---an open source library for Bayesian optimization research. I am particularly interested in practical methods for principled exploration (using probablistic models) that are robust across applied problems and depend on few, if any, hyperparameters. Furthermore, I aim to democratize such methods by open sourcing reproducible code. I completed my PhD at the University of Oxford where I worked with Michael Osborne, and I worked with Finale Doshi-Velez at Harvard University on efficient and robust methods for transfer learning during my master's degree.
In my free time, it's a safe bet that I'm climbing, skiing, running, scuba diving, or scheming about how to get to the remote reaches of the world.Selected Papers
Publications

Bayesian Optimization over Discrete and Mixed Spaces via Probabilistic Reparameterization
Optimizing expensive-to-evaluate black-box functions of discrete (and potentially continuous) design parameters is a ubiquitous problem in scientific and engineering applications. Bayesian optimization (BO) is a popular sample-efficient method that selects promising designs to evaluate by optimizing an acquisition function (AF) over some domain based on a probabilistic surrogate model. However, maximizing the AF over mixed or high-cardinality discrete search spaces is challenging as we cannot use standard gradient-based methods or evaluate the AF at every point in the search space. To address this issue, we propose using probabilistic reparameterization (PR). Instead of directly optimizing the AF over the search space containing discrete parameters, we instead maximize the expectation of the AF over a probability distribution defined by continuous parameters. We prove that under suitable reparameterizations, the BO policy that maximizes the probabilistic objective is the same as that which maximizes the AF, and therefore, PR enjoys the same regret bounds as the underlying AF. Moreover, our approach admits provably converges to a stationary point of the probabilistic objective under gradient ascent using scalable, unbiased estimators of both the probabilistic objective and its gradient, and therefore, as the number of starting points and gradient steps increase our approach will recover of a maximizer of the AF (an often-neglected requisite for commonly used BO regret bounds). We validate our approach empirically and demonstrate state-of-the-art optimization performance on many real-world applications. PR is complementary to (and benefits) recent work and naturally generalizes to settings with multiple objectives and black-box constraints.
Samuel Daulton, Xingchen Wan, David Eriksson, Maximilian Balandat, Michael A. Osborne, Eytan Bakshy.
Advances in Neural Information Processing Systems 35, 2022.
Paper | Code
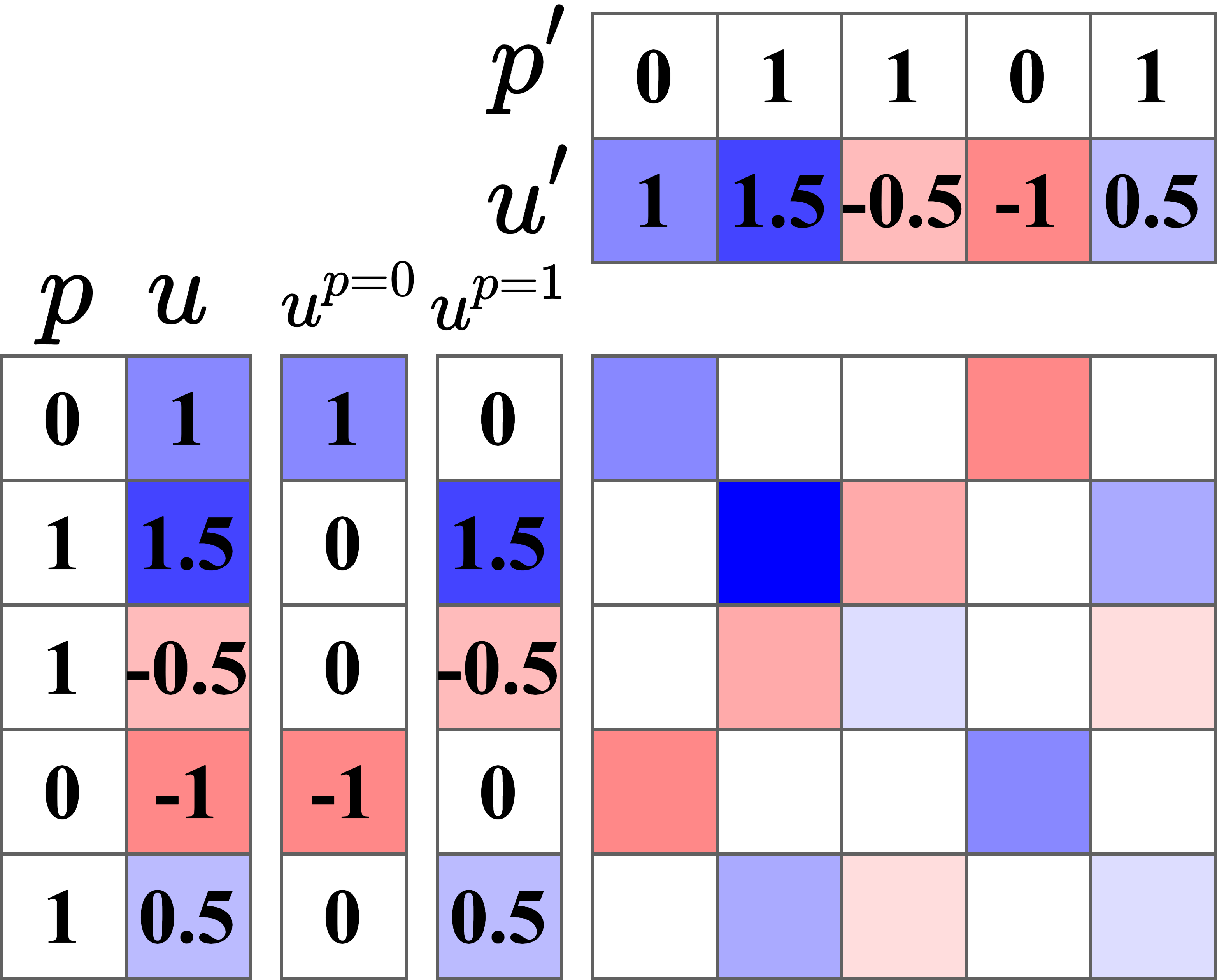
Log-Linear-Time Gaussian Processes with Binary Tree Kernels
Gaussian processes (GPs) produce good probabilistic models of functions, but most GP kernels require cubic time in the number of data points. We present a new kernel that allows for Gaussian process regression in log-linear time. Our "binary tree" kernel places all data points on the leaves of a binary tree, with the kernel depending only on the depth of the deepest common ancestor. We can store the resulting kernel matrix in linear space in log-linear time, as a sum of sparse rank-one matrices, and approximately invert the kernel matrix in linear time. Sparse GP methods also offer linear run time, but they predict less well than higher dimensional kernels. On a classic suite of regression tasks, we compare our kernel against Matern, sparse, and sparse variational kernels. The binary tree GP assigns the highest likelihood to the test data on a plurality of datasets, usually achieves lower mean squared error than the sparse methods, and often ties or beats the Matern GP. On large datasets, the binary tree GP is fastest, and much faster than a Matern GP.
Michael K. Cohen, Samuel Daulton, Michael A. Osborne
Advances in Neural Information Processing Systems 35, 2022.
Paper | Code
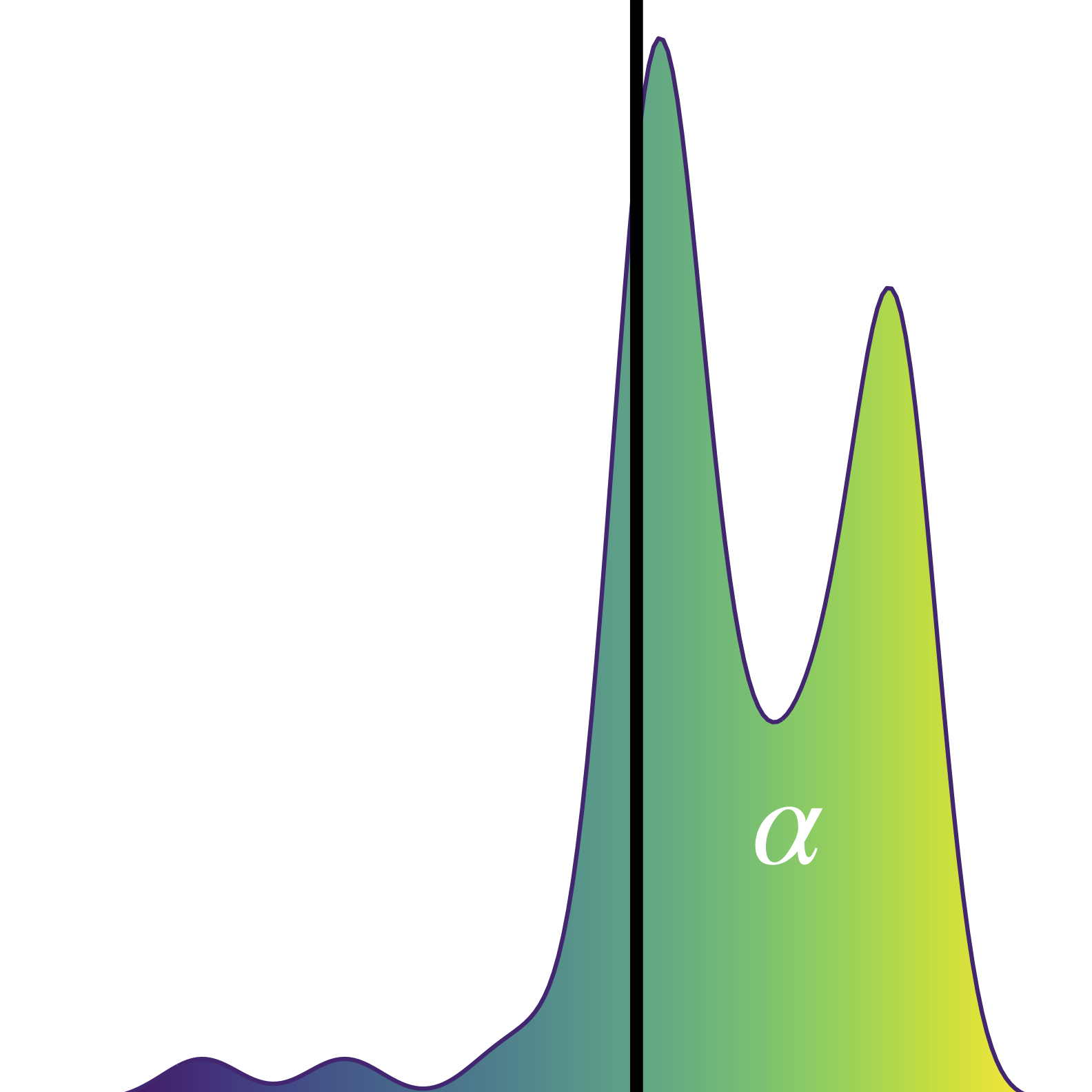
Robust Multi-Objective Bayesian Optimization Under Input Noise
Bayesian optimization (BO) is a sample-efficient approach for tuning design parameters to optimize expensive-to-evaluate, black-box performance metrics. In many manufacturing processes, the design parameters are subject to random input noise, resulting in a product that is often less performant than expected. Although BO methods have been proposed for optimizing a single objective under input noise, no existing method addresses the practical scenario where there are multiple objectives that are sensitive to input perturbations. In this work, we propose the first multi-objective BO method that is robust to input noise. We formalize our goal as optimizing the multivariate value-at-risk (MVaR), a risk measure of the uncertain objectives. Since directly optimizing MVaR is computationally infeasible in many settings, we propose a scalable, theoretically-grounded approach for optimizing MVaR using random scalarizations. Empirically, we find that our approach significantly outperforms alternative methods and efficiently identifies optimal robust designs that will satisfy specifications across multiple metrics with high probability.
Samuel Daulton*, Sait Cakmak* (*equal contribution), Maximilian Balandat, Michael A. Osborne, Enlu Zhou, Eytan Bakshy
Proceedings of the 39th International Conference on Machine Learning, 2022.
Paper | Code | Talk
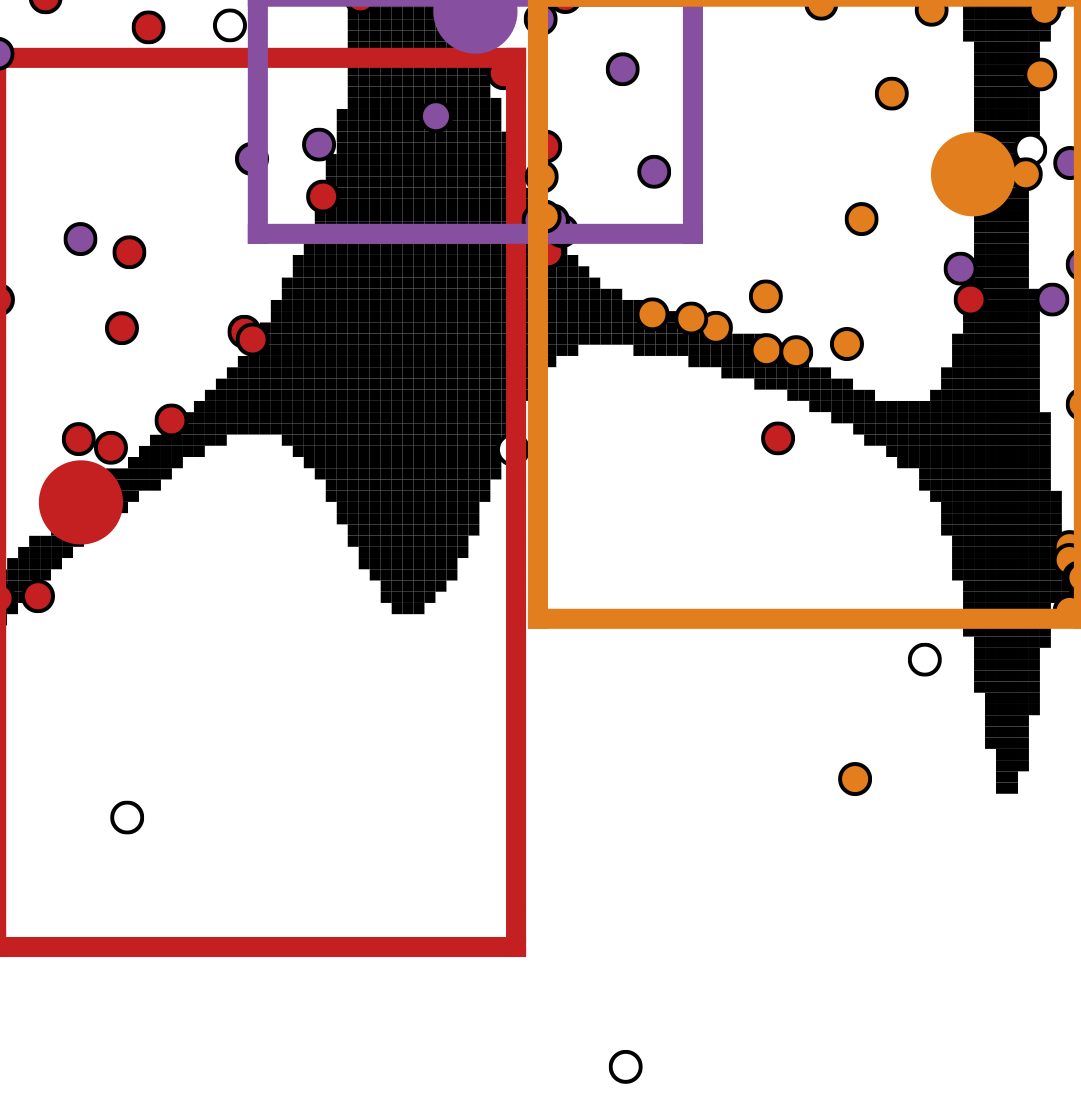
Multi-Objective Bayesian Optimization over High-Dimensional Search Spaces
The ability to optimize multiple competing objective functions with high sample efficiency is imperative in many applied problems across science and industry. Multi-objective Bayesian optimization (BO) achieves strong empirical performance on such problems, but even with recent methodological advances, it has been restricted to simple, low-dimensional domains. Most existing BO methods exhibit poor performance on search spaces with more than a few dozen parameters. In this work we propose MORBO, a method for multi-objective Bayesian optimization over high-dimensional search spaces. MORBO performs local Bayesian optimization within multiple trust regions simultaneously, allowing it to explore and identify diverse solutions even when the objective functions are difficult to model globally. We show that MORBO significantly advances the state-of-the-art in sample-efficiency for several high-dimensional synthetic and real-world multi-objective problems, including a vehicle design problem with 222 parameters, demonstrating that MORBO is a practical approach for challenging and important problems that were previously out of reach for BO methods.
Samuel Daulton*, David Eriksson* (*equal contribution), Maximilian Balandat, Eytan Bakshy
[Oral]
Proceedings of the 38th Conference on Uncertainty in Artificial Intelligence, 2022.
Paper | Code
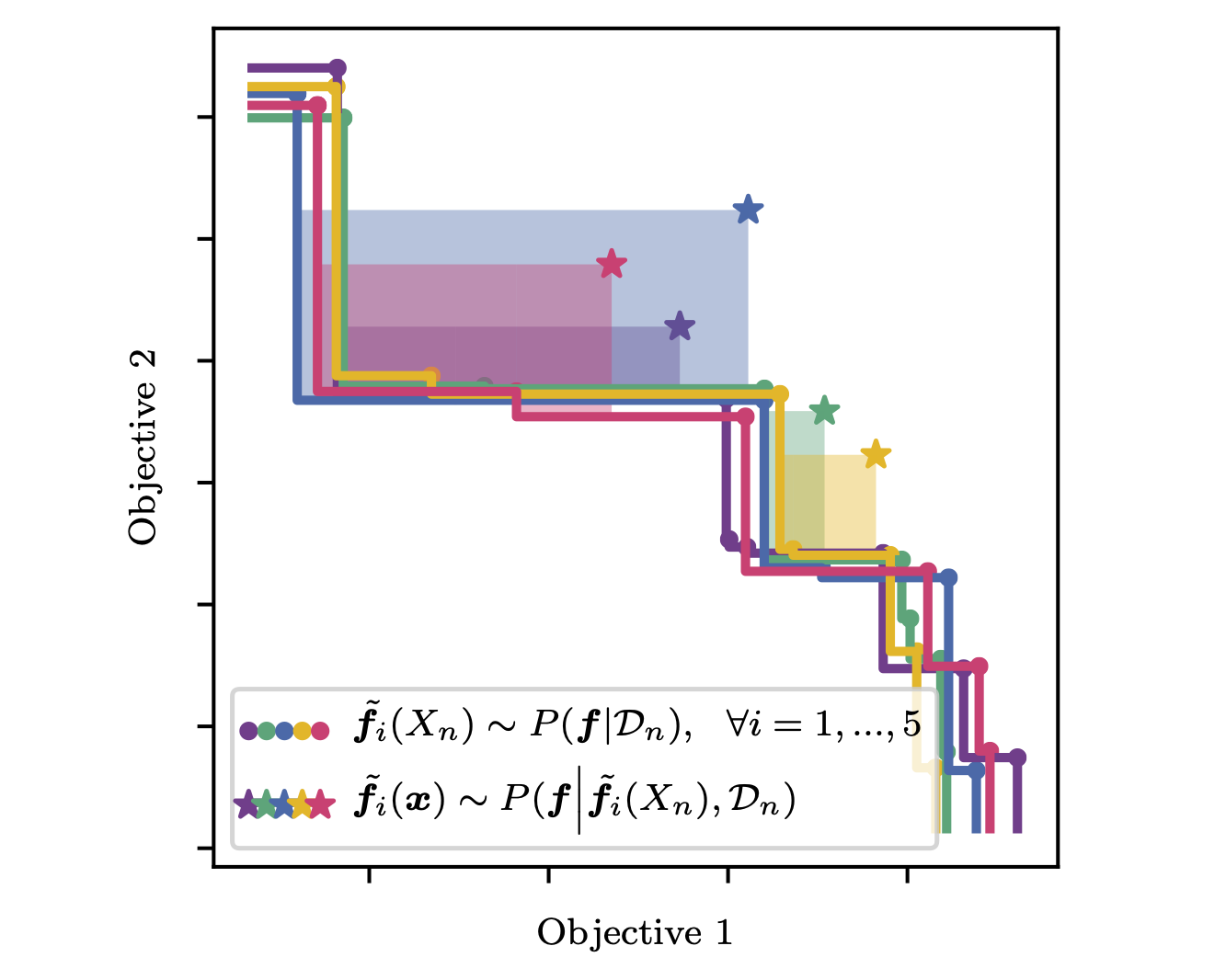
Parallel Bayesian Optimization of Multiple Noisy Objectives with Expected Hypervolume Improvement
Failure to account for noisy observations at the previously evaluated designs can degrade optimization performance and lead to clumped solutions on the Pareto frontier.To address this issue, we propose a new acquisition function q-Noisy Expected Hypervolume improvement (qNEHVI) that takes a Bayesian approach and integrates over the unknown function values at the previously evaluated points. qNEHVI is one-step Bayes optimal in noisy and noiseless environments (in the latter it is equivalent to expected hypervolume improvement). Although the iterated expectation in qNEHVI is intractable and computing qNEHVI involves computationally intensive, non-differentiable box decompositions, we show that qNEHVI can be efficiently estimated by caching the box decompositions (CBD) once per Bayesian optimization iteration and using sample-average approximation. Furthermore, we show how CBD can be used for efficient generating batches of candidate designs and reduces time/space complexity from exponential to polynomial in the batch size. We demonstrate state-of-the-art performance in sequential optimization, and we find that qNEHVI performs best regardless of the batch size.
Samuel Daulton, Maximilian Balandat, Eytan Bakshy
Advances in Neural Information Processing Systems 34, 2021.
Paper | Code | Video
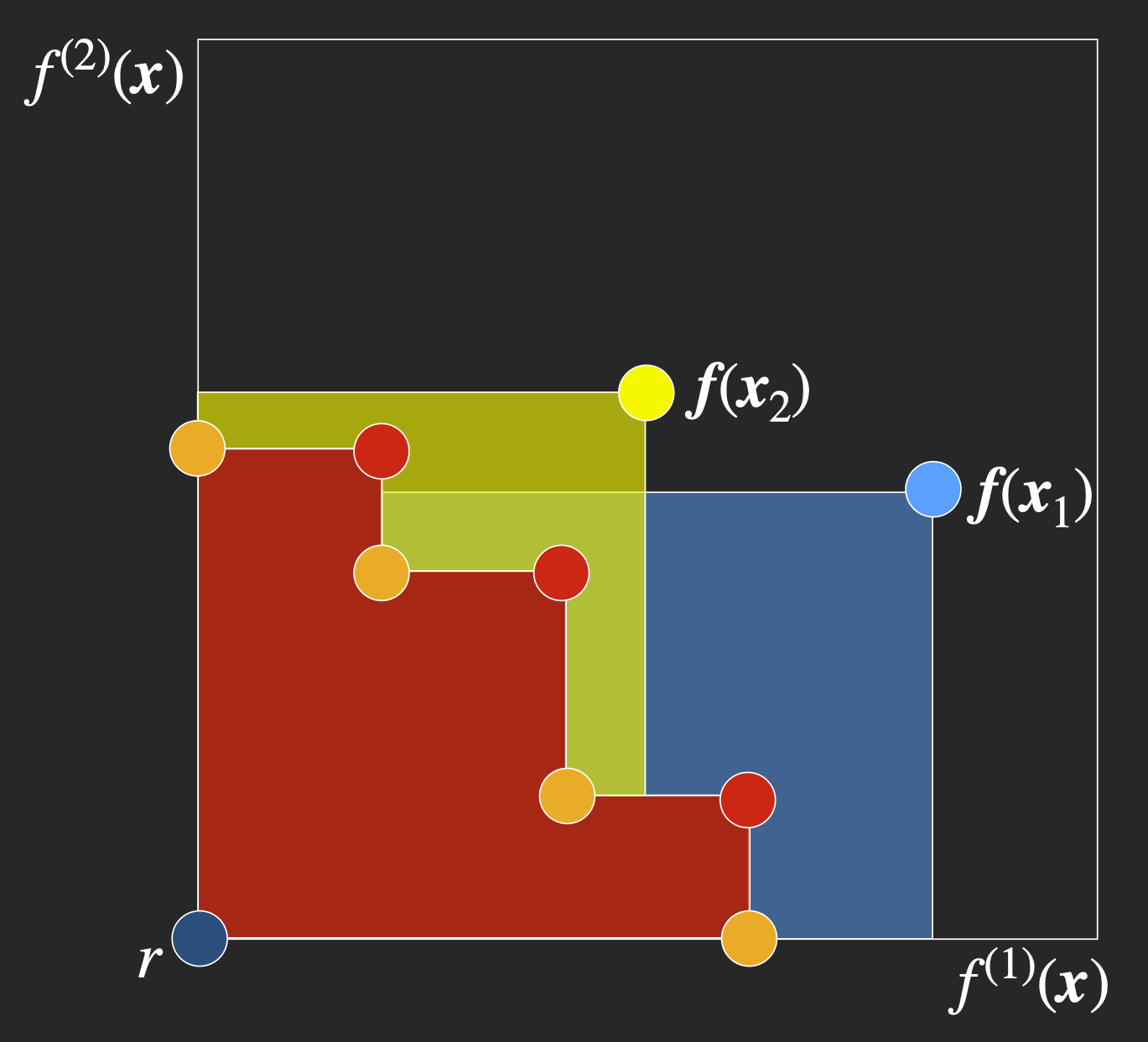
Differentiable Expected Hypervolume Improvement for Parallel Multi-Objective Bayesian Optimization
We propose a new state-of-the-art acquisition function for constrained Bayesian optimization of multiple competing objectives. The acquisition function is an exact calculation of expected hypervolume improvement other than monte-carlo integration error. It enables parallel (batch) evaluations via the inclusion-exclusion principle, and it is differentiable, which enables efficient gradient-based acquisition optimization. We prove that the sample average gradient of the Monte-Carlo acquisition is an unbiased estimator of the gradient of the true expected hypervolume improvement.
Samuel Daulton, Maximilian Balandat, Eytan Bakshy
Advances in Neural Information Processing Systems 33, 2020.
Paper | Code | Video

BoTorch: Programmable Bayesian Optimization in PyTorch
We propose a modular Monte-Carlo-based framework for developing new methods for Bayesian optimization. We include multiple examples including a novel one-shot optimization formulation of the Knowledge Gradient. We provide convergence guarantees for a broad class of quasi-Monte-Carlo acquisition functions using the sample average approximation.
Maximilian Balandat,
Brian Karrer,
Daniel Jiang,
Samuel Daulton,
Benjamin Letham, Andrew Gordon Wilson, Eytan Bakshy
Advances in Neural Information Processing Systems 33, 2020.
Paper | Code
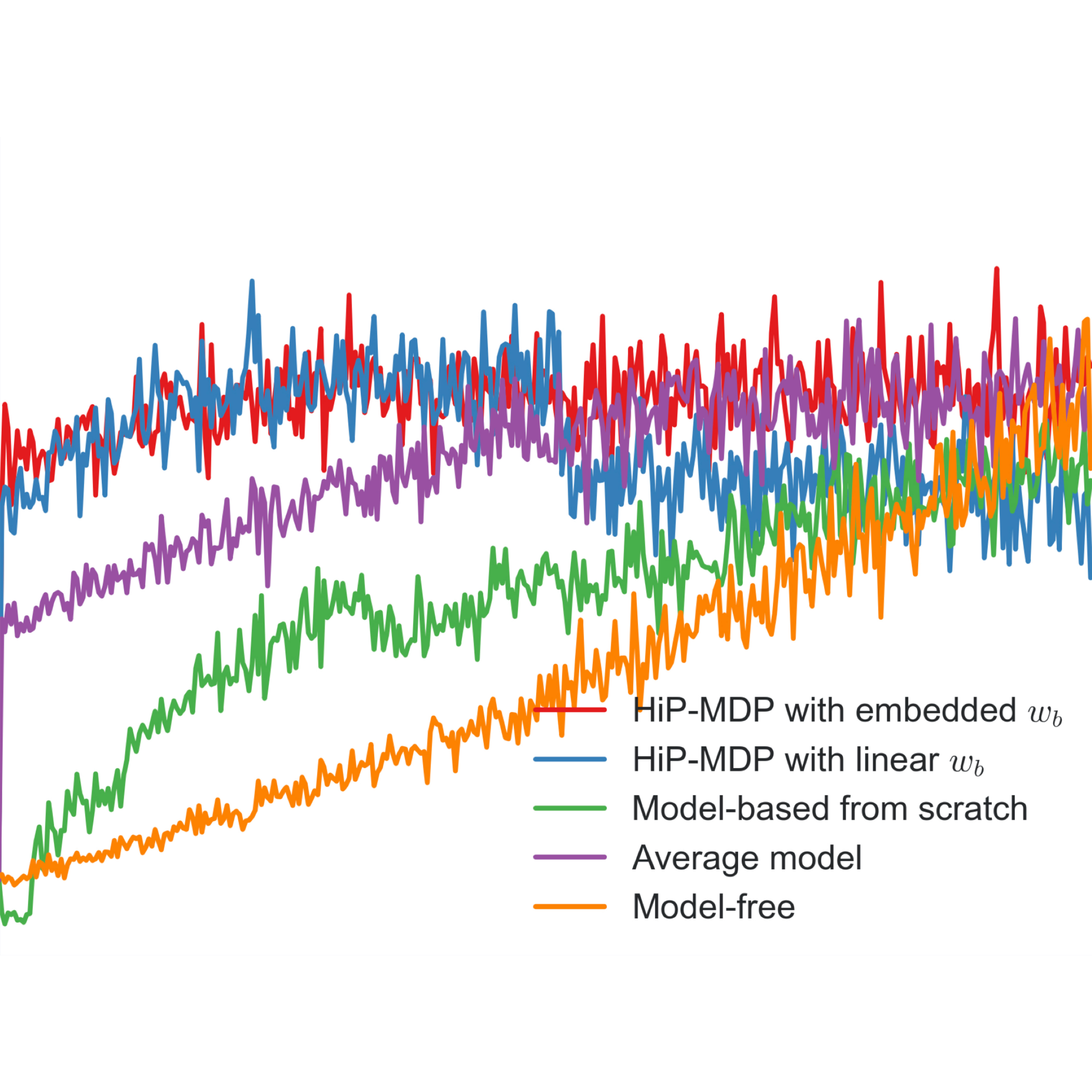
Robust and Efficient Transfer Learning with Hidden Parameter Markov Decision Processes
We propose a novel algorithm for transfering knowledge between similar, but different reinforcement learning tasks by learning low-dimensional latent embeddings. These embeddings encode task-specific nuances and are provided with the state and action as the input to transition model that is shared across task instances. Modeling the dynamics with a Bayesian neural network enables scalable inference and joint optimization of the network parameters and latent embeddings.
Taylor W. Killian*,
Samuel Daulton* (*equal contribution),
George Konidaris, Finale Doshi-Velez
[Oral] Advances in Neural Information Processing Systems 30, 2017.
Paper | Code
Refereed Workshop Papers
Latency-Aware Neural Architecture Search with Multi-Objective Bayesian Optimization
When tuning the architecture and hyperparameters of large machine learning models for on-device deployment, it is desirable to understand the optimal trade-offs between on-device latency and model accuracy. In this work, we leverage recent methodological advances in Bayesian optimization over high-dimensional search spaces and multi-objective Bayesian optimization to efficiently explore these trade-offs for a production-scale on-device natural language understanding model at Facebook.
David Eriksson*, Pierce I-Jen Chuang*, Samuel Daulton* (*equal contribution), Peng Xia, Akshat Shrivastava, Arun Babu, Shicong Zhao, Ahmed Aly, Ganesh Venkatesh, Maximilian Balandat.
ICML Workshop on Automated Machine Learning, 2021.
Paper

Distilled Thompson Sampling: Practical and Efficient Thompson Sampling via Imitation Learning
We propose a practical method for distilling a Thompson sampling policy into a compact, explicit policy representation for contextual bandit optimization in applications with limited memory and low-latency requirements. The expensive posterior sampling and numerical optimization is performed offline, while the imitation policy is used for efficient online decision-making. We show that our method enjoys the same Bayes regret as the best UCB algorithm, up to a sum of single time step approximation errors, which can be easily controlled with abudant "unlabeled" contexts (without an action or reward) that are available in many practical applications (e.g. firms typically have databases with features about different entities).
Hongseok Namkoong*, Samuel Daulton* (*equal contribution), Eytan Bakshy
[Oral] NeurIPS Offline Reinforcement Learning Workshop, 2020.
Paper | Video | Talk

Thompson Sampling for Contextual Bandit Problems with Auxiliary Safety Constraints
We consider a new class of contextual bandit problems with constraints on auxiliary outcome(s). We consider upper confidence bound and Thompson sampling-based algorithms and perform ablation studies revealing nice properties regarding fairness using the Thompson sampling algorithm. We demonstrate the performance of the algorithm on a real world video transcoding problem.
Samuel Daulton, Shaun Singh, Vashist Avadhanula, Drew Dimmery, Eytan Bakshy
NeurIPS Workshop on Safety and Robustness in Decision Making, 2019.
Paper
Talks

Practical Solutions to Exploration Problems
I discuss many practical approaches we use at Facebook for principled exploration including policy optimization with Bayesian optimization via online experiments, constrained Bayesian optimization, multi-task Bayesian optimization accelerated with offline simulations, and contextual bandits.
Samuel Daulton
Netflix ML Platform Meetup on Exploration and Exploitation, 2019.
Video | Slides